30天挑战数据结构和算法之第6、7天快速排序

October 23 2019

本期的挑战主题是快速排序，我打算分两天来完成。先是关于快速排序理论知识的学习。今天发现visualgo.net上还有一个e-Lecture Mode，上面有关于每种算法详细的讲解。

快速排序是应用分治思想的另一种实现方式。上一篇中的归并排序也是利用分治思想的体现。

分解：选择一个元素p作为中枢，然后把数组a[i..j]分解成三部分：a[i..m-1]，a[m]以及a[m+1..j]。

其中，a[i..m-1]包含了小于元素p的元素集合。a[m]就是中枢元素p，而a[m+1..j]则包含了大于等于元素p的元素集合。

然后，递归排序这两部分。

解决：你没看错，这部分什么都不做。

分解思维

为了分解数组a[i..j]，我们首先选择a[i]作为中枢元素p。剩下的元素被分解为三部分

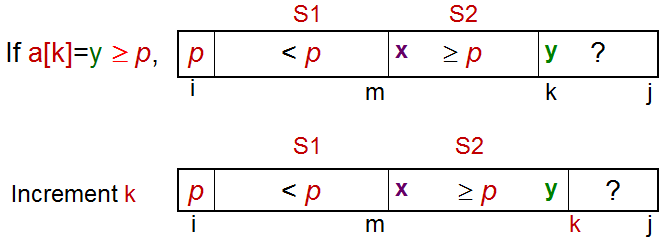
  1. S1 = a[i+1..m]，小于元素p的部分
  2. S2 = a[m+1..k-1]，大于等于元素p的部分
  3. Unknown = a[k..j]，未知部分，将被分配到S1或S2中

刚开始的时候，S1和S2都是空数组。未知部分包含了除元素p以外的所有元素。

接下来，对于每个在未知部分的a[k]元素，我们比较a[k]和p元素的大小，来决定将a[k]元素放入哪个数组里

  1. 如果a[k] >= p，将a[k]放入S2数组中

  2. 如果a[k] < p，将a[k]放入S1数组中

最后，我们通过交换a[i]和a[m]，将中枢元素p放入数组S1和S2的中间。

a[k] >= p的情况

a[k] < p的情况

代码实现

javascript版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function MyQuickSort() {
	this.partition = function(a, i, j) {
		var p = a[i];
		var m = i;
		for(var k = i+1; k <= j; k++) {
			if(a[k] < p) {
				m++;
				var temp = a[k];
				a[k] = a[m];
				a[m] = temp;
			}
		}

		var temp = a[i];
		a[i] = a[m];
		a[m] = temp;

		return m;
	}

	this.sort = function(a, low, high) {
		if (low < high) {
			var m = this.partition(a, low, high);
			this.sort(a, low, m-1);
			this.sort(a, m+1, high);
		}
	}
}

var sorter = new MyQuickSort();
var list = [7, 8, 1, 5]
sorter.sort(list, 0, list.length);
console.log(list);
ruby版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def partition(a, i, j)
	p = a[i]
	m = i
	(i+1).upto(j) do |k|
		if a[k] < p
			m = m + 1
			a[k], a[m] = a[m], a[k]
		end
	end

	a[i], a[m] = a[m], a[i]

	return m
end

def my_quick_sort(a, low, high)
	if low < high
		m = partition(a ,low, high)
		my_quick_sort(a, low, m-1)
		my_quick_sort(a, m+1, high)
	end
end

list = [7, 8, 1, 5]
my_quick_sort(list, 0, list.size - 1)
print list, "\n"
Java版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import java.util.Arrays;

public class MyQuickSort {
	public static int partition(int a[], int i, int j) {
		int p = a[i];
		int m = i;
		for(int k = i+1; k <= j; k++) {
			if(a[k] < p) {
				m++;
				int temp = a[k];
				a[k] = a[m];
				a[m] = temp;
			}
		}

		int temp = a[m];
		a[m] = a[i];
		a[i] = temp;

		return m;
	}

	public static void sort(int a[], int low, int high) {
		if(low < high) {
			int m = partition(a, low, high);
			sort(a, low, m - 1);
			sort(a, m + 1, high);
		}
	}

	public static void main(String[] args) {
		int[] a = {7, 8, 1, 5};
		sort(a, 0, a.length - 1);
		System.out.println(Arrays.toString(a));
	}
}

时间复杂度

首先是最优时间复杂度。假设以pivot为中枢的元素，在执行partition操作时每次都划分得很均匀。此时可以得到一个不等式T(n) <= 2T(n/2) + O(n)，就跟上一篇中求归并算法的平均时间复杂度一样，得出最优时间复杂度为T(n) = O(nlgn)，以2为底的对数。

其次是最差时间复杂度。假设序列为已经排序好的正序序列或倒序序列，每次执行partition划分操作只得到一个比上一次划分操作少一个记录的子序列，另一个为空。此时的时间复杂度公式为T(n) = (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2。也就是说最差时间复杂度为T(n) = O(n^2)。

最后是平均时间复杂度。公式为
$$
T(n)=\frac1n\sum^{n}{k=1}(T(k-1)+T(n-k)) + n=\frac2n\sum^{n}{k=1}T(k)+n
$$
可以求得平均时间复杂度为T(n) = O(nlgn)。

空间复杂度

空间复杂度主要是递归操作对栈内存的使用。最优情况下，递归树深度为lgn，空间复杂度为O(lgn)。最差情况下，需要进行n-1次递归，空间复杂度为O(n)。平均情况下，空间复杂度也为O(lgn)。

总结

快速排序不算是一种稳定的算法，它取决于每次选择的中枢pivot的值是否均衡，从最差时间复杂度和最优时间复杂度上就能得到体现。和归并排序一样都用到了分治思想，用递归的方式去将原问题分解为较小的子问题，在分解的过程中，问题会迎刃而解。

avatar

chilihotpot

You Are The JavaScript In My HTML