30天挑战数据结构和算法之第11、12、13天dijkstra最短路径

October 29 2019

因为开始了最短路径算法的学习，索性把比较容易入门的dijkstra算法理论篇给看了一遍，主要参考自通俗易懂理解——dijkstra算法求最短路径一文。

先上图，求从D开始到各点的最短距离。

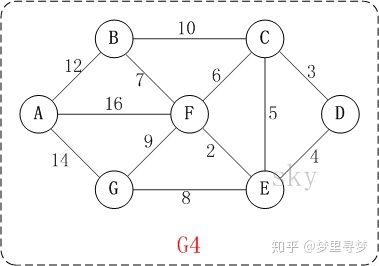
1、初始化距离，指与D直接连接的点的距离。假设dis[C]代表D到C的最短距离，那么可以得到dis[C]=3，dis[E]=4，dis[D]=0，其它点为无穷大。集合S表示已经找到的最短距离。dis[D]=0最短，也就是D点自身，得到集合S={D}。此时D到各点的最短距离可以表示为{D(0), C(3), E(4), F(*), G(*), B(*), A(*)}，*代表无穷。

2、不考虑集合S中的值D，dis[C]=3就是最短的距离。更新集合S，S={D,C}。接着看和C相连的点分别有B、E、F，已经在集合S中的不考虑。因而可以得到dis[B]=dis[C]+dis[C-B]=3+10=13，dis[F]=dis[C]+dis[C-F]=3+6=9，dis[E]=dis[C]+dis[C-E]=3+5=8>4（dis[E]初始值为4），所以E点不更新。此时D到各点的最短距离更新为{D(0), C(3), E(4), F(9), G(*), B(13), A(*)}。

3、不考虑集合S中的C、D，dis[E]=4就是最短的距离。更新集合S，S={D,C,E}。此时与E相连的点分别有F、G，已经在集合S中的不考虑。因而可以得到dis[F]=dis[E]+dis[E-F]=4+2=6<9（上一步中求出dis[F]为9），F点需要更新。dis[G]=dis[E]+dis[E-G]＝4+8=12。因此，D到各点的最短距离更新为{D(0), C(3), E(4), F(6), G(12), B(13), A(*)}。

4、不考虑集合S中的元素，剩余dis[F]=6最小，更新集合S，S={D,C,E,F}。和F相连的点分别有B、A、G，已经在集合S中的不考虑。因而可以得到dis[B]=dis[F]+dis[F-B]=6+7=13（和上一步中的dis[B]持平，不替换），dis[A]=dis[F]+dis[F-A]=6+16=22，dis[G]=dis[F]+dis[F-G]=6+9=15>12（不更新）。此时，D到各点的最短距离更新为{D(0), C(3), E(4), F(6), G(12), B(13), A(22)}。

5、不考虑集合S中的元素，剩余dis[G]=12最小，更新集合S，S={D,C,E,F,G}。和G相连的只有A。可以得到dis[A]=dis[G]+dis[G-A]=12+14=26>22（不更新）。因此，D到各点的最短距离更新为{D(0), C(3), E(4), F(6), G(12), B(13), A(22)}。

6、不考虑集合S中的元素，剩余dis[B]=13最小，更新集合S, S={D,C,E,F,G,B}。和B相连的只有A，已经在集合S中的不考虑。可以得到dis[A]=dis[B]+dis[B-A]=13+12=25>22（不更新）。因此，D到各点的最短距离更新为{D(0), C(3), E(4), F(6), G(12), B(13), A(22)}。

7、最后只有点A没有加入集合S了，将其加入后得到集合S={D,C,E,F,G,B,A}。此时，所有点都遍历完毕，得到最终结果为{D(0), C(3), E(4), F(6), G(12), B(13), A(22)}。

以上就是dijkstra最短路径算法，我们可以归纳一下基本思想。以下都是我摘抄的

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

操作步骤如下

初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为”起点s到该顶点的距离”[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

从U中选出”距离最短的顶点k”，并将顶点k加入到S中；同时，从U中移除顶点k。

更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

重复步骤(2)和(3)，直到遍历完所有顶点。

总结

这个算法拖了我好几天了，加上工作的关系，今天必须有个结束。虽然我还没用代码实现，只是纯理论的讲解，但是也让我对dijkstra算法有了一个算是初步的认识。

从明天起，应该是一些数据结构的学习了，算法这一篇章先到此为止。